
乮1972擭12寧7擔丄傾億儘17崋偵搵忔偟偨僴儕僜儞丒僔儏儈僢僩巵偑嶣塭偟偨抧媴乯
丂丂抧媴偺嬻婥憌偺岤偝
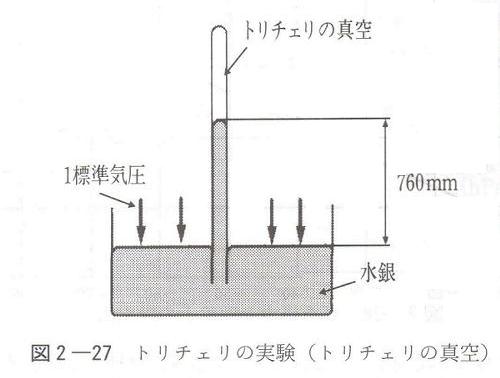
丂抧媴偺宍忬偼媴宍丄偦偺敿宎偼俇俁俈侽倠倣偁傞丅偦偟偰偦偺忋偵嬻婥偺憌傪揨偭偰偄傞丅偱丄偦偺暘岤偝偼丠栺俆侽倠倣偱偁傞丅偦傟偼惉憌寳偺忋晹偲尵傢傟傞偲偙傠偱偦偙偺嬻婥偺敄偝偼抧忋晹偺栺1/1000偱偁傞丅偡側傢偪抧媴偺敿宎偺0.78亾丄傕偟敿宎侾侽們倣偺墌傪昤偄偨偲偟偰傕嬻婥偺憌偼0.8mm偱侾倣倣偵傕側傜側偄丅偦傟傎偳敄偭傌傜偄懚嵼偱偁傞丅
丂嬻婥偺廳偝乮幙検乯
丂偄傑丄侾cm亊侾cm掙柺愊傪帩偪丄嬻婥偑側偔側傞忋嬻乮栺100km忋嬻亖嬻婥偺擹偝偼抧忋晅嬤偺侾侽侽枩暘偺侾埵乯傑偱怢傃偰偄傞嬻婥偺拰傪峫偊丄偦偺拞偺嬻婥偺幙検傪應傞偲偄偔傜偵側傞偐丅
丂摎偊偼1.033kg偱偁傞丅忋偺傛偆側婥拞偺幙検傪捈愙應偙偲偼晄壜擻偱偁傞偑娫愙揑偵應傞曽朄偑偁傞丅
 丂
丂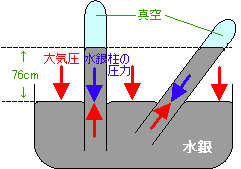
傑偢丄悈嬧傪枮偨偟偨梕婍傪恾偺傛偆偵梡堄偡傞丅
傑偨丄娗偺曅曽偑暵偠傜傟偰偄傞栺侾倣偺挿偝偺僈儔僗娗傪梡堄偡傞丅
偙偺僈儔僗娗偵悈嬧傪枮偨偟丄悈嬧偑楻傟側偄傛偆偵巜偱墴偝偊偰丄梡堄偟偨悈嬧棴傔偺悈嬧偺拞傑偱擖傟偰巜傪偦偭偲娚傔傞偲僈儔僗娗偺拞偺悈嬧偺偄偔傜偐偼悈嬧棴傔偵弌傞偑丄僈儔僗娗撪偺悈嬧偼慡晹弌傞偺偱偼側偔偁傞崅偝傑偱壓偑傞偲偦傟埲忋偼壓偑傜側偔側傞丅
偙偺幚尡偼僈儔僗娗偺抐柺愊偵娭學側偔悈嬧拰偺崅偝偼摨偠偱俈俇cm偱偁傞偑丄夝傝傗偡偔偡傞偨傔偵丄娗撪柺愊偑侾cm2偺僈儔僗娗偲偟偰榖傪恑傔傞丅
偙偺拞偵偁傞悈嬧偺幙検亖悈嬧拰偺懱愊亊悈嬧偺枾搙
丂亖侾cm2亊俈俇cm亊侾俁.俆俋g乛cm3
丂亖侾侽俁俁倗亖侾.侽俁俁kg
偙偺1033g偺悈嬧偵廳椡偑摥偒惗偢傞椡偼
丂俥亖倣倗亖幙検亊廳椡壛懍搙亖侾.侽俁俁[倠倗]亊俋.俉[倣乛倱2]亖侾侽.侾俁[俶]
偙偺椡偑侾cm2偵偐偐偭偰偄傞偺偱
丂俹亖侾侽.侾俁[俶乛cm2]亖10.13亊10000乵俶乛倣2亖俹倎乶
丂丂亖101300[俹倎]亖1013[倛俹倎]亖101.3[倠俹倎]亖0.1013[俵俹倎]
丂偙偺傛偆偵丄嬻婥拰偺拞偺嬻婥偺幙検偼應傟側偐偭偨偑丄悈嬧傪巊偆偙偲偱應傞偙偲偑弌棃傞丅
悈嬧偺枾搙偼侾俁.俆俋g乛cm3偱丄戝婥埑偵憡摉偡傞悈嬧拰偼俈俇們倣偱偁傞丅偙傟傪俈俇們倣俫倗偲昞偡丅
丂悈偺枾搙偼侾.侽g乛cm3偱偁傞偐傜丄戝婥埑傪悈拰偱昞偡偲侾侽.俁俁倣俙倯偲側傞丅俙倯偼(aqua)偱丄悈傪堄枴偡傞丅偙偙偱偼悈拰傪堄枴偡傞丅
- 偙傟傜偐傜
| 戝婥埑 | 亖侾侽侾俁hPa乮透氖呓顿乯婥徾娭學偱巊傢傟偰偄傞 亖侽.侾侽侾俁MPa亖侾侽侾.俁kPa 亖俈俇cmHg亖俈俇侽mmHg 亖侾侽.俁俁mAq 亖侾.侽俁俁Kg乛cm2丂廳椡扨埵宯偱尰嵼偼巊傢傟側偄 |